

今天跟某位期权交易的高人交谈了一下,他比较推崇这本书。
在专栏暂停之前,写了一篇关于这本书的读书笔记。
后来在交易的时候,遇到了很多以前单维度交易都没遇到过的问题。
最后发现Dynamic Hedging这本书还是需要好好啃啃。
蓝鹅本屌的英文实在太渣,基本上是边看边查单词的状态。
因此还是先把文章开头发在这里,督促一下自己早点啃完第一章。
(待续……)
========= 正式开始 =========
自己的理解和看不懂的部分我会用大括号{}标注
衍生品是一种,其价格最终取决于标的价格的证券。
然后根据最终Payoffs,衍生品可以分为两个大类:线性衍生品和非线性衍生品。
所谓非线性衍生品,就是存在该衍生品的价格对于影响其价格的某个参数的二阶导数(曲率、凸性)。
下图是书中关于衍生品分类的树形图。
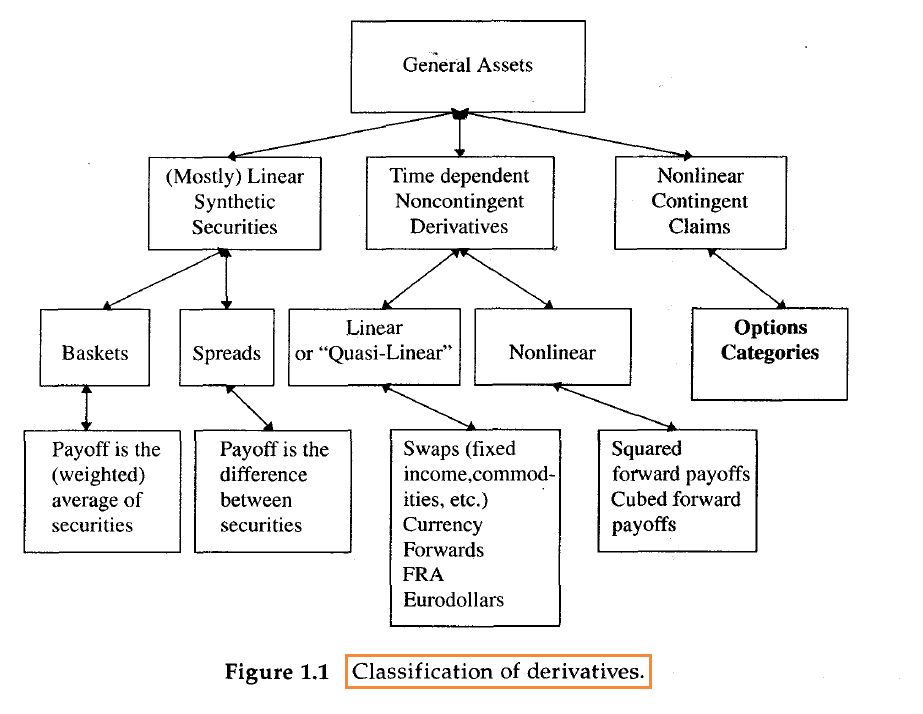
图中的分类比起线性和非线性的分类稍微细化了一点:
一般衍生品可以在上述两大分类的基础上继续细分:
其中3,就是我们说的(广义)期权。
欧式期权就是非线性衍生品的一种,欧式期权的价格对于标的价格的二阶导数就是我们常说的Gamma。
书中提到一个风险管理规则:所有非线性衍生品的价格均受到时间的影响,即Contamination Principle(传染定理?该怎么翻译比较妥当……)。
也就是说,假如存在某非线性衍生品的价格 V = V(S),那么它一定可以写成关于时间的函数:V = V(S, t)。也即是说,所有的Gamma(或者说凸性)都会伴随着时间的衰减。{二者之间有什么必然联系吗?至今不解。}
这里要注意一点:从对冲交易员的角度来看,期权的价格就是用现货复制的成本。因此对于交易员来说,他并不会关心持有的期权到底是看涨还是看跌,他只关注执行价和到期日。(当然还有波动率。)
并且,线性衍生品由于没有凸性,因此是(几乎)不需要动态对冲的。
1. 线性合成证券
线性合成证券几乎都不会呈现出凸性(除了某些比较特殊的合成规则,比如几何平均)。
2. 受时间影响的线性衍生品
这一类衍生品会根据时间的不同而呈现出不同的Payoff,但是都是线性的。
这种衍生品个人感觉有点像时间的分段函数的意味,不同的时间间隔(t, t+1)对应的Payoff不一样,但是其结构都是线性的。
这一小节提及到一个关于动态对冲的重要的定理:传染定理(Contamination Principle)。
对于某衍生品,假如在标的价格和时间的构成的空间里,有某一点能带来交易利润,那么这一点的邻近领域也对该交易利润作出了贡献。{其实我只看懂了大概,试着翻译一下吧……}
受时间影响的先行衍生品主要包括:远期、FRA、欧洲美元、互换。
这里需要注意的是:
互换有时候需要考虑到资产之间的相关性。
债券期货某程度上其实是属于期权。{由于CTD券存在的缘故、}
上述两类均被归类到线性衍生品的范畴。
1. 受时间影响的非未定权益
这类衍生品会体现出某种凹凸性,但是它们并非未定权益。书中举的一个例子是LIBOR - Square,即LIBOR的平方。
之所以说这类品种不属于未定权益,是因为这类产品的买卖双方到期末都有义务履行合约。
2. 期权以及其他未定权益
何谓未定权益?未定权益的意思是指,衍生品买卖双方的权利和义务是不对等的。
然后后面介绍了一系列的基本概念。
值得注意的有两点:一是期权是一种考虑计价单位的衍生品。
比如一个马克兑美元的看跌期权,就是一个美元兑马克的看涨期权。
收益率的看跌期权就是债券(价格)的看涨期权。
二是关于内在价值(Intrinsic value)
一般对于欧式期权来说,交易员会把内在价值看成是标的在到期日的远期价格减去执行价。
这是由于欧式期权只能在到期日执行价。
有具体执行价的衍生品我们称之为硬性选择权,没有具体执行价但是又具有Gamma特性的衍生品我们称之为软性选择权(比如债券期货内嵌的CTD券选择权)。
不管是软性还是硬性,选择权是值钱的,不同的选择权对应不同的权利金。同时,选择权的价格会随着时间的流逝而减少。
比如期权平价定理,这里用的是标的的远期合约。其实只需要记住,通过Call和Put可以合成标的远期就可以了,其他的都是通过等式移项得出。
需要注意的是:对于美式期权,由于提前执行价的条款,平价理论是不成立的。(所以目前国内的商品期货期权是不能使用期权平价定理。)
由期权平价定理可以推出镜像定理:
一单位的Put + x%单位的远期 = 一单位的看涨 + (100 - x%)单位的远期。
镜像定理的推导是根据期权的delta来。
对于欧式期权对冲而言,由于只能在到期日执行,因此使用的应该是forward delta 而非 cash delta。
风险管理规则:对于期权平价公式,不应该在不同执行价的时候使用。对于某些具有软性美式特性的期权而言,当delta太大的时候平价公式不再适用{为什么?是因为要考虑Vega凸性吗?}
书中根据提前执行所需考虑的成分,把美式期权分成软美式和硬美式。
软美式是指,是否提前行权只受到基于内在价值的融资成本的影响。
硬美式是指,是否提前行权会受到基于内在价值的融资成本和交割后持有标的资产的持有成本的影响。
也就是说,软美式期权是否提前执行的判断标准是:马上行权获得的内在价值进行再投资获得的收益,是否大于期权的总价值。假如是,则提早行权是有利的。
硬美式是否提前执行的判断标准的:马上行权获得的内在价值进行再投资获得的收益 + 持有标的资产产生的持有成本,是否大于期权的总价值。
{这里,是否可以这么理解:所有以现金交割的美式期权均为软美式,所有以标的资产交割的美式期权均为硬美式?假如是这样的话,目前国内上市的期权均是硬美式期权。但是书中又说到,期货期权是软美式期权。是由于期货的Carry cost为零?}
需要注意的是,由于硬美式期权在提前执行的时候需要考虑到融资利率和持有成本,因此很多硬美式期权持有者都不会选择提前执行,因此硬美式期权会退化成欧式期权。
{原谅我的渣英语,原文写着soft American options will be largely similar to the European options except when interest rates become very high relative to volatility,我没看明白到底是“利率和波动率高度相关”、还是“利率具有相对高的波动”?}
{之前知乎上有人提问说美式期权应该怎么对冲,其实这里已经有简化的答案。}
关于美式期权的价格,Taleb大师说了这么一句话:
Never trust the price for an American option on a cash instrument.
{只见Taleb一掌打出,对学术界研究美式期权的人构成了一记暴击……}
{因为各种影响现金流的变量比如利率、红利率之类的是极度不稳定的,这些参数会通过影响融资成本来影响是否提前执行进而影响美式期权的价格。}
===========
冼尼玛
2017/07/10
=========== Pure Delta · 专栏目录 ===========