一点读书笔记。
由于工作需要，最近都在沉迷Q系的书籍。
重新翻看了Shreve的二册神书以及Paul Wilmott的Quant Finance。
不得不说，好的数学教材确实能让人走少更多弯路。
在我初学金融工程的时候，根本不知道Ito Lemma到底是怎么一回事——为什么我们需要这个引理？
其实细看过这两本教材的朋友都应该知道，伊藤引理伟大之处在于：它是连接随机变量（或者说随机过程）与微积分的桥梁。
有了伊藤引理，让随机过程的微积分成为可能。
今天这篇专栏，就简单梳理一下书上的笔记。
以下内容在《Stochastic Calculus for Finance II》与《Paul Wilmott on Quantitative Finance》两本书上都能找到。
1. 布朗运动的构造
让我们从抛硬币开始。
假设有这么一个游戏，抛硬币，假如硬币出现正面（以H表示）赢一元，出现反面（以T表示）输一元，那么，每次的胜负就是一个随机变量：
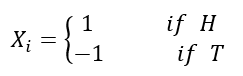定义
为了直观理解，让我们画个图。假设我们抛十次硬币。最终赢得的金钱M的走势如下图所示：
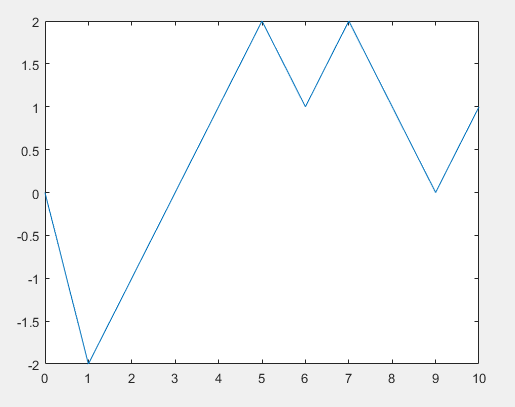（嗯运气比较一般，10次下来才赢一块钱……）。
好了，现在让我们加速抛硬币的进程，单位时间内抛25次，同时把单次赌注压缩为
（这样抛硬币在现实中有可能致残，本训练经过专人指导，专栏前的观众切勿模仿）
现在最终赢得的金钱M，走势如下图所示：
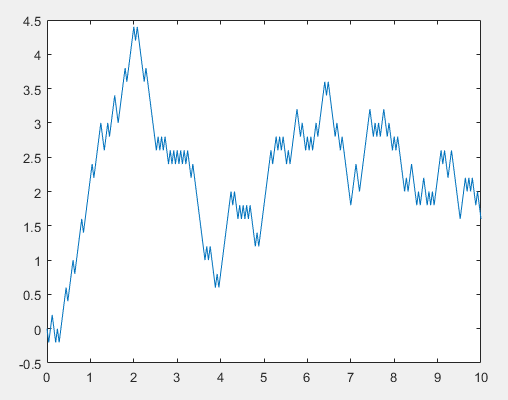
最后我们试一下单位时间内抛1600次硬币：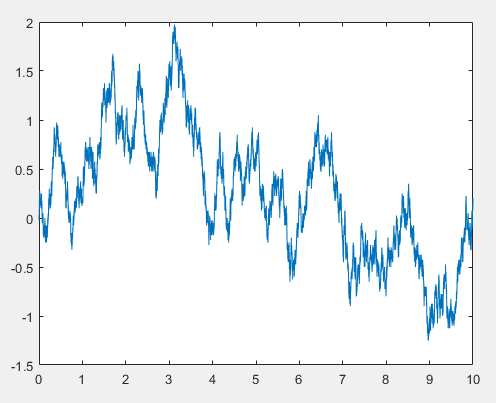
随着n的不断增大，我们就可以通过抛硬币构造了一个布朗运动。
假如我们构造了很多条这样的路径，比如这样（其中横轴为时间）：
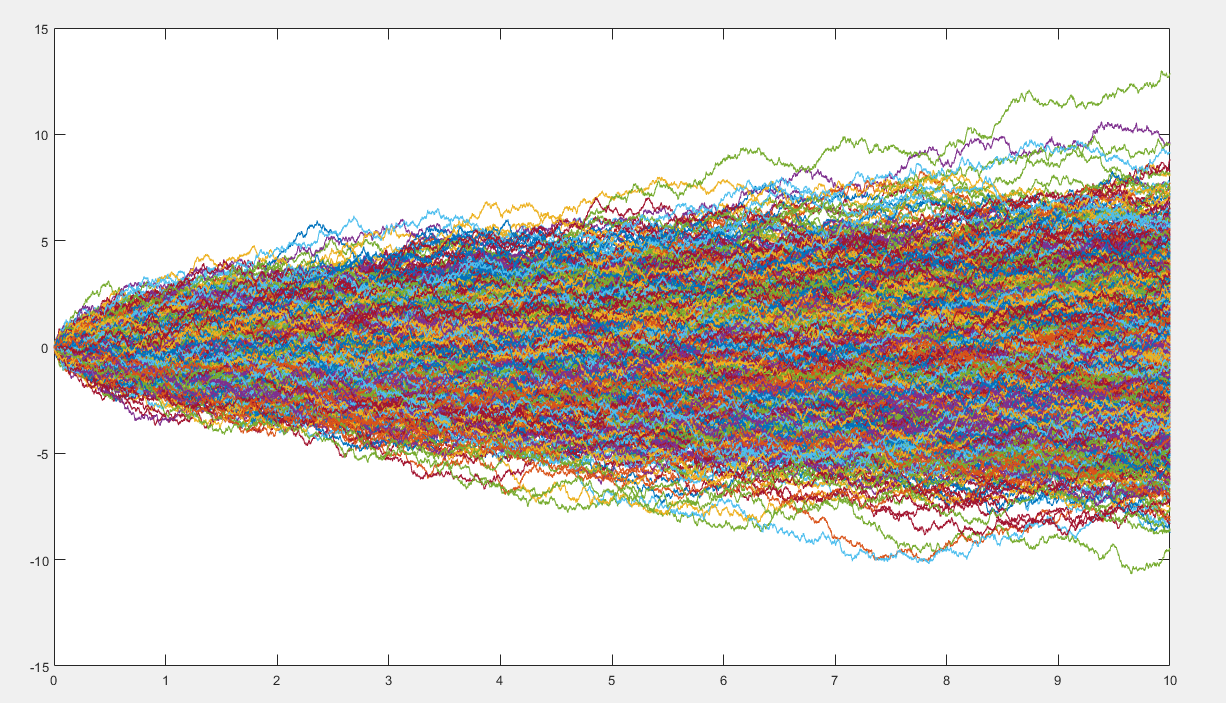
假如我们固定横坐标的某一点t0，一刀切下去，得出的横截面数据，其频率直方图（随着抛硬币次数的增多）会逼近于正态分布：
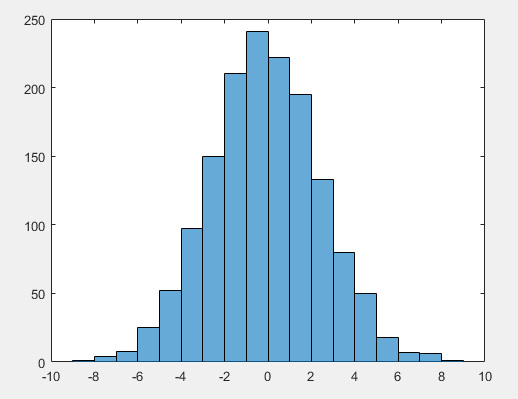
2. 几何布朗运动与二次变差
有了布朗运动之后，很多学金融的人就想：能不能把布朗运动作为股价运行的假设条件啊？于是一开始我们就有了下式：
其中dS为瞬时股价变动，u为股票的预期收益率，σ是股票的波动率，X是上面说的一个标准布朗运动。
那么股票的走势就可以分解成预期收益率（确定性）与波动率（随机性）两个部门，这么弄看起来好像不错啊。
然而这个假设有个问题：S有可能为负数。
于是我们又有了如下的天才假设：把股票的收益率看成是服从正态分布的：
在这个假设下，股价就不为负了。
那么假如我要解这条微分方程，那是否可以直接通过以前的微积分学去解呢？也就是说是否可以直接把上式积分：
答案是，不行。
在传统的黎曼积分下，基本假设是被积变量是处处连续并且可导的。
而布朗运动，虽然它是一个关于时间的函数，但是dW/dt并不存在，即布朗运动关于时间t是连续的，但是不可导。
这个问题可以通过二次变差来说明。
初等函数的二次变差可以通过下式表示：
可以证明，具有连续导数的初等函数，其二次变差为零，因此普通微积分学从来不会考虑二次变差。（具体证明请参考Shreve第二册第三章，利用到中值定理。）
而对于布朗运动，其在时间T上累积的二次变差恰好等于T。也就是说布朗运动对于时间t是不可导的，那要怎么构建布朗运动上的微积分呢？
这个时候，大名鼎鼎的伊藤清出现了。
3.伊藤引理
上文说了，伊藤引理的伟大之处在于，它是连接随机变量与微积分之间的桥梁。
举个例子：
假设X(t)是一个布朗运动，
详细的计算和伊藤引理的证明可参见《Paul Wilmott on Quantitative Finance》第一册第四章，这里不再赘述。
结论：如果X(t)是一个布朗运动，F是X的函数，那么：
证明的大概思路是：在对随机变量构成的函数进行泰勒展开后，由于二次变差存在的缘故，因此在对随机变量的函数进行微分时，要考虑到二阶项
在姜礼尚《期权定价的数学模型和方法》里，其中有一段话是这么说的：
如果不建立原生资产价格的运行模型，对于期权定价的讨论只可能是定性的，无法定量，也就是说，如果要给衍生品——期权定价，必须要进一步给出原生资产价格演化的具体模型。
有了伊藤引理，就可以对标的价格运动路径进行定量的分析了。
（顺便说一句，如果没有几何布朗运动的假设，对期权的研究最多只能推导出期权平价公式，有兴趣的各位不妨一试。）
冼尼玛
2016/12/19
=========== 交易员崛起 · 专栏目录 ===========