
又到年末,应酬聚会工作之类的又开始多起来,讲的无非也就回忆当年勇展望未来时之类的话题。
想想自己做(不合格的)场外期权研究也快一年的时间了。当时找工作的时候也就想要是找不到期权相关的工作我就安分的去做个柜员好了。最后也是想不到自己居然从事了量化领域中用工需求最小的pricing quant。
现在每天推导各种数学模型,旁人看来觉得有点不可思议想着你这都是什么工作天天面对这一堆符号,自己却找回了久违的学习数学的快乐,这种乐趣大概也就只有对数学感兴趣的人才明白吧。
看多事情感觉上天早有安排,自己心中也常怀感恩。
又到校招时,希望各位最后都有个好的归宿。
走到山穷处,坐看云起时。
====== 题外话说完 ======
====== 以下是正文 ======
作为场外期权组的成员之一,除了欧式期权之外,经常接触到一些比较特殊的需求,对于Exotic Options的研究也是重点工作之一。
而亚式期权,应该是场外期权领域里,期权买卖双方都比较青睐的一种Exotic。
之所以这么说是由于,对于期权买方而言,相比起欧式,亚式的对冲难度要稍微小一点(然并卵,看看最近国内商品期货的波动率)。对于期权卖方而言呢,期权费用要比欧式便宜。
今天就来说一下亚式期权。
一般我们说的亚式期权都是以平均价作为特征的期权,根据均价作用的变量,可以将亚式期权分为两大类:标的价平均 或者 执行价平均,执行价平均的亚式期权我没研究过,不好乱说,下文主要是说标的价平均的亚式期权。
学过金融工程的朋友都知道,期权的期初价格都可以表示成期权期末Payoffs的期望的折现值,亚式期权的价格就可以表示成下式:
其中期权类型为Call时w=1,期权类型为Put时w=-1。
根据均值计算方法的不同,亚式期权又可以分为几何平均亚式期权和算术平均亚式期权。
几何平均:
算术平均:
简单起见,我们就以两期均价作为计算例子:
值得注意的是,当期权尚未运行到均价取样点范围时,亚式期权的期末支付如上式。当期权运行到只剩下一个均价取样点的时候,亚式期权退化为普通的欧式期权:
在标的资产价格服从GBM的假设下,由于n个标的价进行几何平均后依然服从对数正态分布,因此几何平均亚式期权是有闭解的。对于几何平均亚式期权感兴趣的朋友可以自行百度(推导过程还是挺有趣的)。
下文主要是讨论算术平均下的亚式期权。
相比起几何平均价,由于标的价格的算术平均价并不存在“简单”的分布函数,因此,算术平均亚式期权并不存在闭解。
不过,服从对数正态分布的随机变量之间的和式,可以近似看成对数正态分布。而且,在描述对数正态分布的性质时,只需要通过求得对数正态分布的期望(一阶矩)和方差(二阶矩)后,该对数正态分布的性质就大致可以得到很好的描述。因此学术上通常都是采用数值逼近的方法计算算术平均价下的亚式期权价格。
常见的算术平均亚式期权定价方法有Turnbull – Wakeman逼近法,Levy逼近法,Curran逼近法。
其中Turnbull – Wakeman逼近法和Levy逼近法较为类似,都是通过逼近算术平均价A(t)的一阶矩和二阶矩之后代入到BSM定价模型求得期权价格。Curran逼近法是通过将期望积分下的关于几何分布的条件期望的积分分拆成两部分,通过数值近似的方法求得期权价格。
(接下来如果来劲了就把Curran的推导更新在这里,今天先放几张图。)
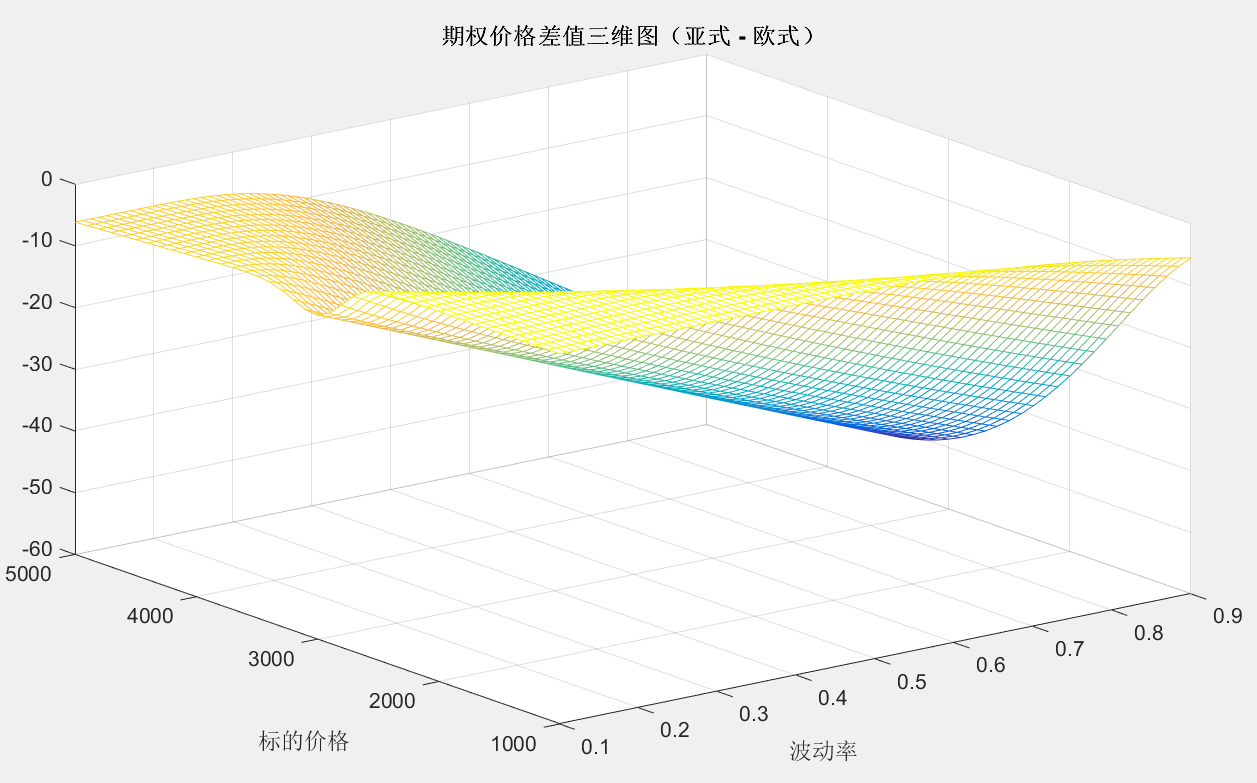
价格:亚式期权在波动率比较大的时候,要比同类型的欧式要贵。
Delta:执行价附近,亚式的delta比欧式delta要“陡”,也就是说,执行价附近亚式的gamma风险比较大。
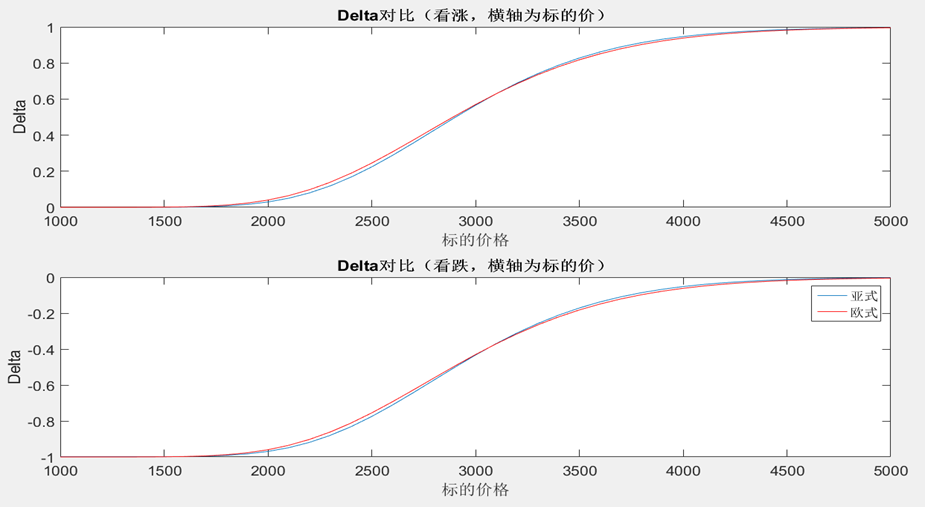 事实上在波动率较小的时候,delta的差异也是集中在执行价附近。
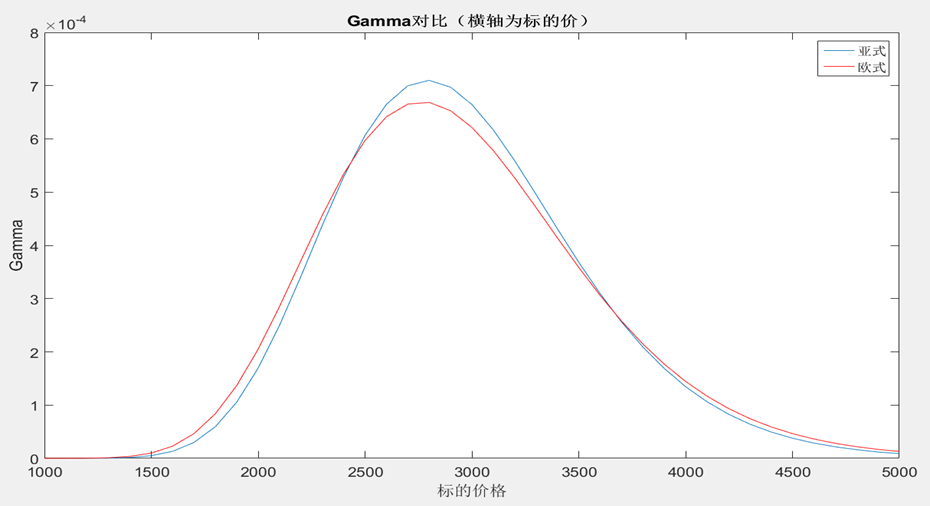
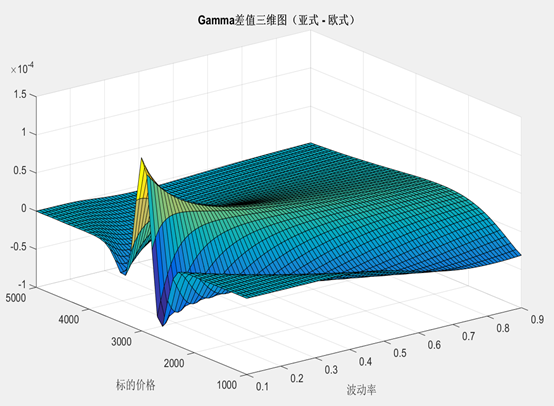
事实上在波动率较小的时候,delta的差异也是集中在执行价附近。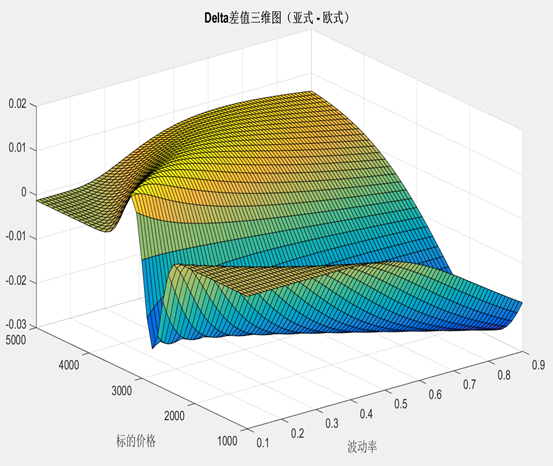 Gamma:主要还是执行价附近的Gamma风险。
Gamma:主要还是执行价附近的Gamma风险。
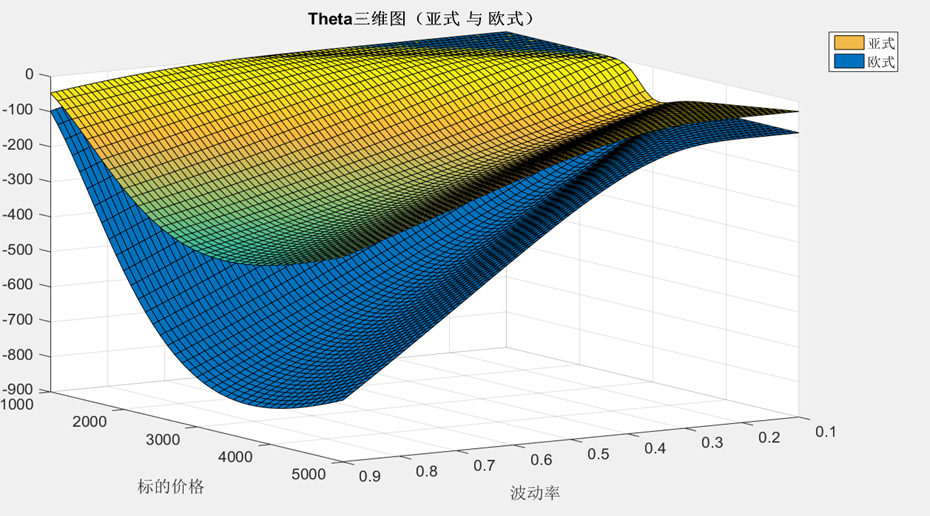
 Theta:比欧式要小。
Theta:比欧式要小。
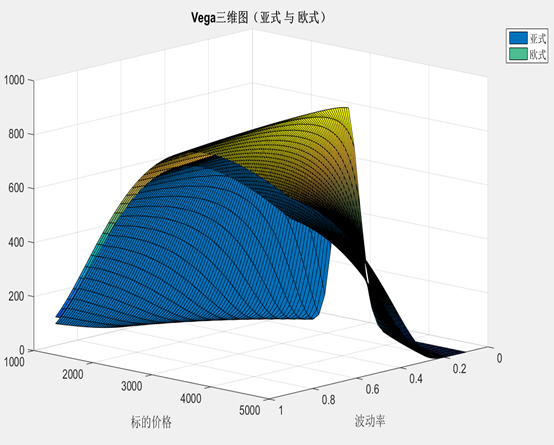
 Vega:
Vega:
(未完待续)
冼尼玛
2016/09/02
=========== 交易员崛起 · 专栏目录 ===========