（图多、慎点。）
前一阵子期权组来了几名实习生，帮我们做一些基础研究工作。交流的过程中发现实习生们对于Delta对冲的认知还是有点蒙逼。
于是写下此文，以后用作培训普及之用。
---
在量化研究（六）中提到了，BSM期权定价公式，实际上就是运用了Delta对冲的思想。
通过用现货来动态复制期权头寸，从而使得整个组合无风险。
这里有两个问题值得注意：（1）为什么可以通过现货复制期权？（2）为什么是Delta对冲？
关于第一个问题，金融学中有一个概念，叫“完备市场”。
大概意思是，如果一个市场的完备的，那么这个市场上所有的衍生品都可以通过现货来进行复制。BSM期权定价公式里面的假设其实就已经内含了完备市场的假设。
关于第二个问题，由于期权是收益非线性的衍生品，非线性的特点，导致期权价格变动和标的价格变动并不是线性变化的关系。在量化研究（六）里面提到，期权的瞬时收益可以通过泰勒分解展开：
在实际中，由于现货本身是没有高阶项导数的，因此在复制的时候会出现偏差。这个在量化研究（六）里已经说过，不再赘述。
今天这篇专栏就通过模拟回测来谈谈Delta对冲的盈亏分布。
初始条件如下：
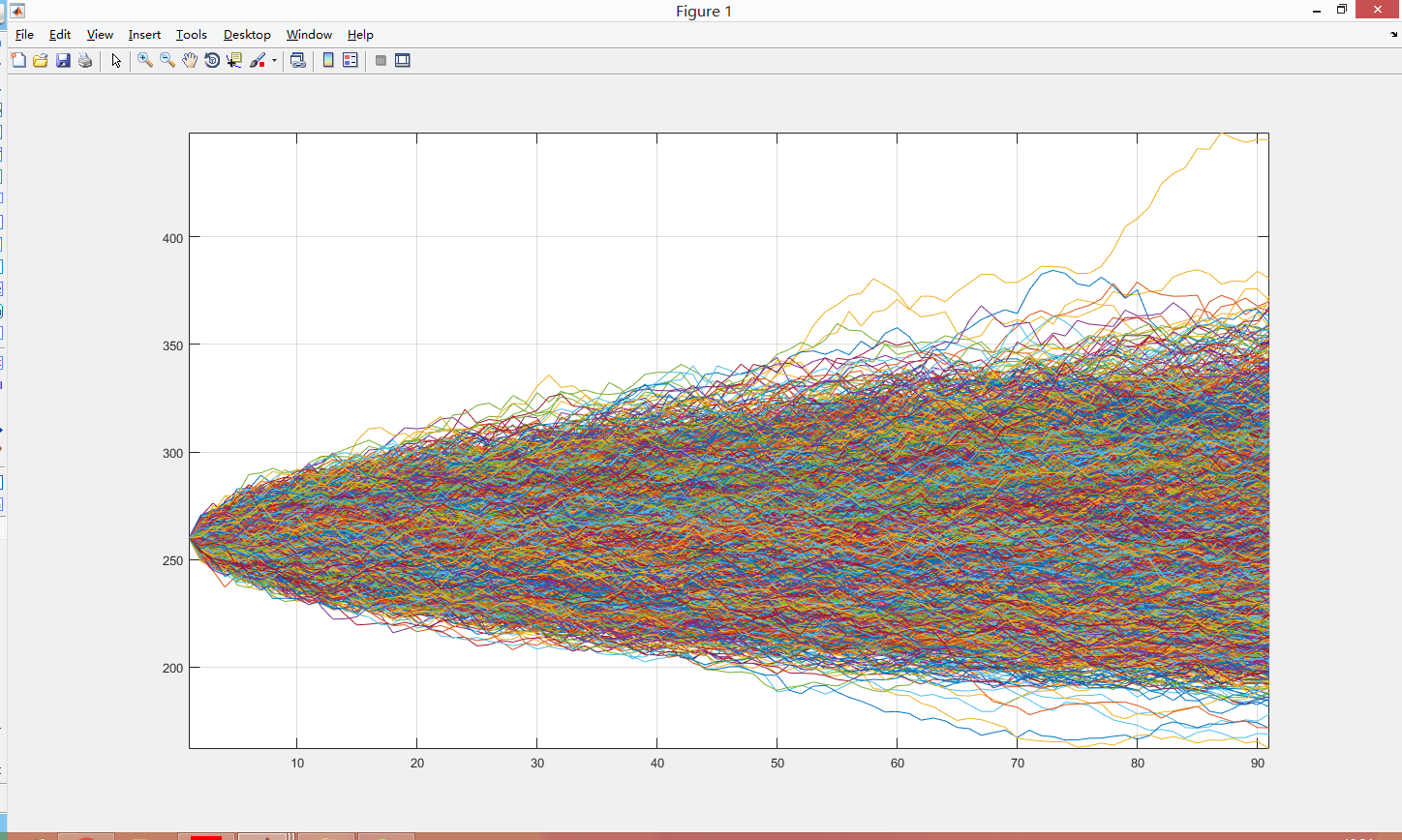
通过GBM运动与常数波动率生成的路径如下图示（一万条路径）：
根据上述路径，计算出期权的价格与delta。
接下来以期权卖方的视角进行分析，假设我们卖出的是ATM期权。
我们知道，看涨期权买方的期末Payoff是长这个样子的：
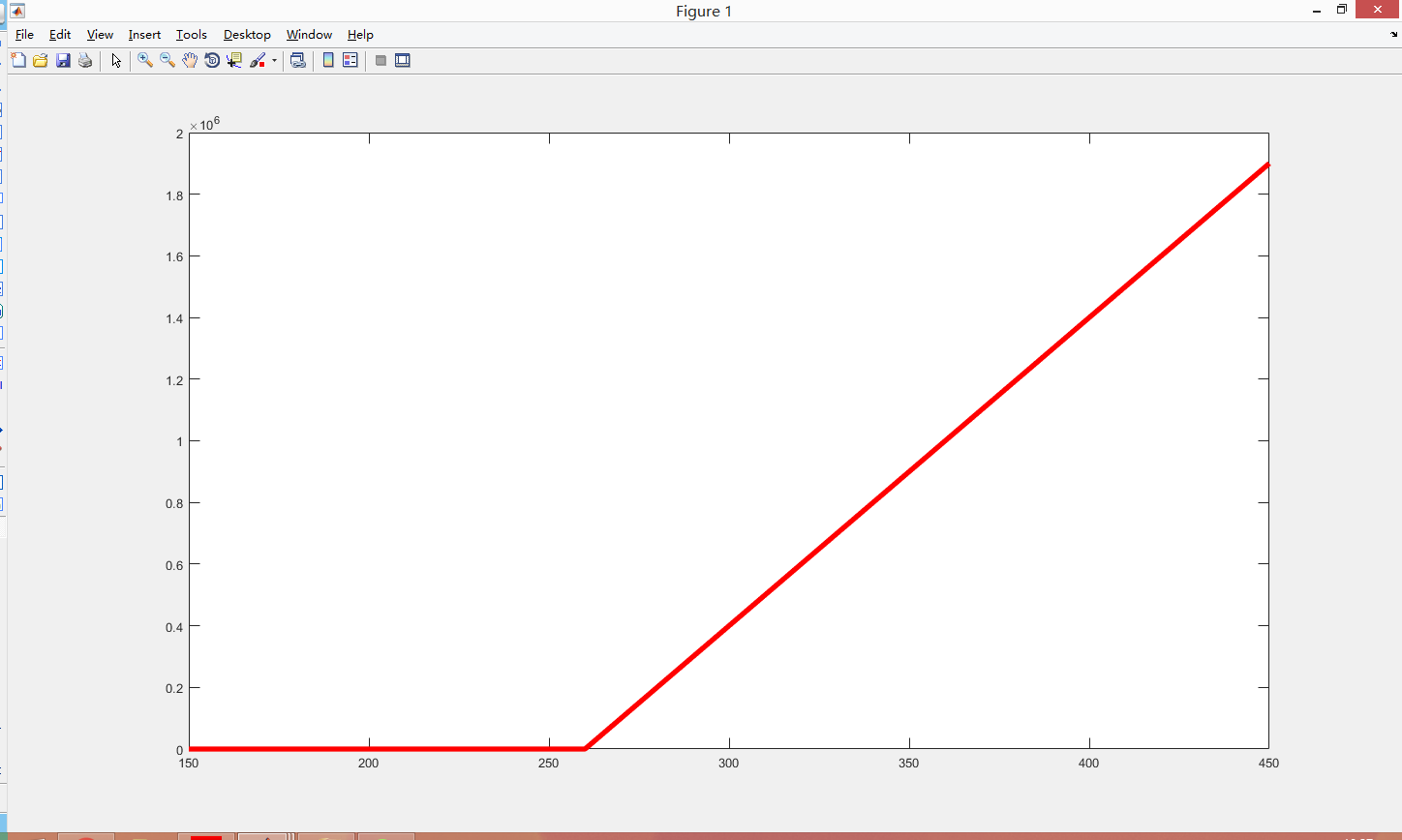由于我们是期权的卖方，因此，通过现货复制期权的复制头寸也应该是上图的样子。
这里说一下：由于期权卖方收取的权利金是大概率不足够覆盖现货的保证金，因此在对冲的时候需要借贷，整个现货组合的市值扣除借贷的金额就等于现货复制期权的复制头寸。
先考虑通过股票来复制的情况，交易单位是1股/手。
在到期日，复制的情况如下图所示：
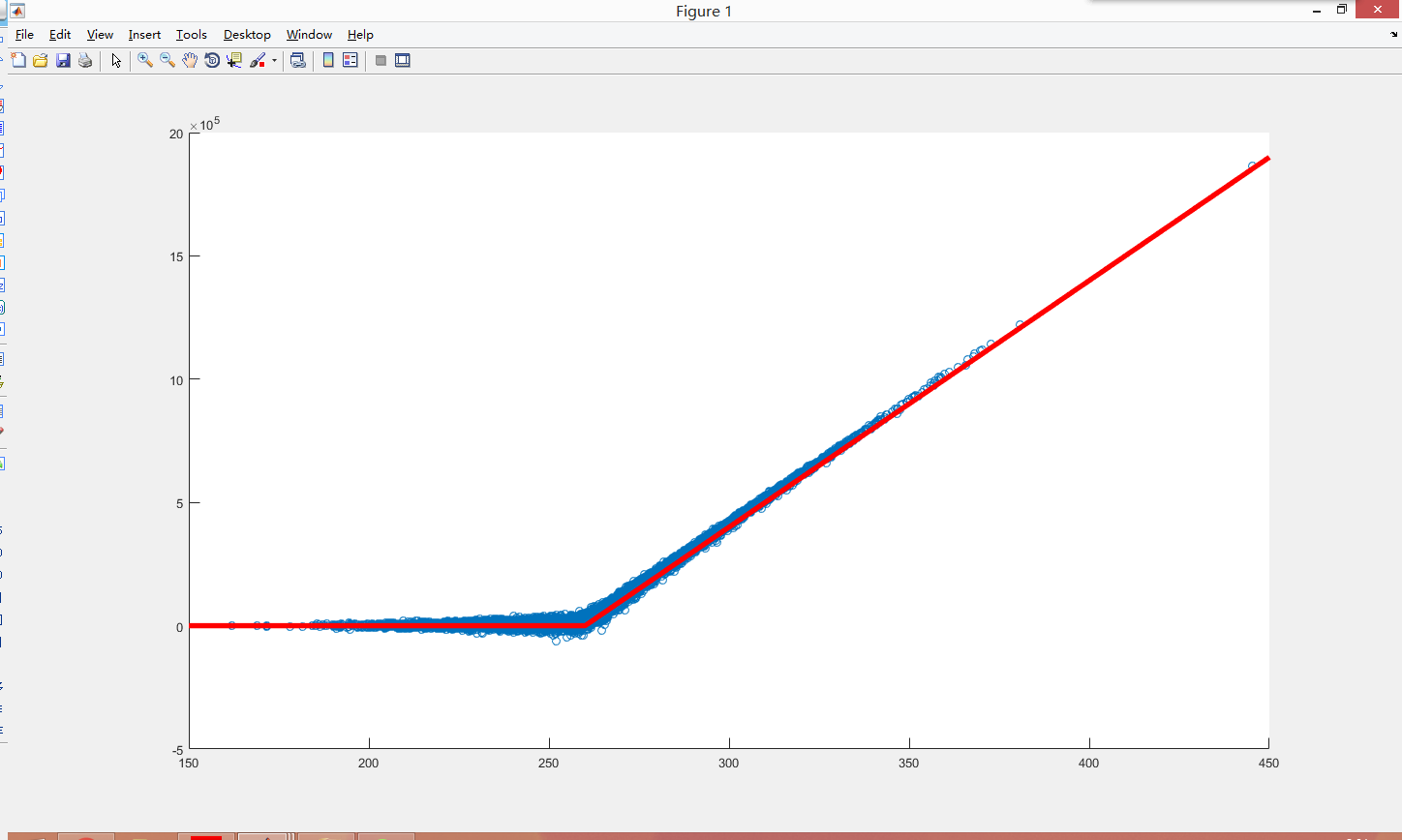
蓝色的点就是现货复制头寸的期末盈亏状况，可以看到，散点图几乎和期权的期末payoff曲线吻合。这里我们可以看到两个问题：
1. 执行价两端的情况出现较少，也即是说，极端盈亏情况出现较少。
2. 执行价附近的离散情况比较严重，即复制误差较大。
根据图示，复制后，整个资产组合的盈亏大概会长得像正态分布的样子。
事实上如图示：
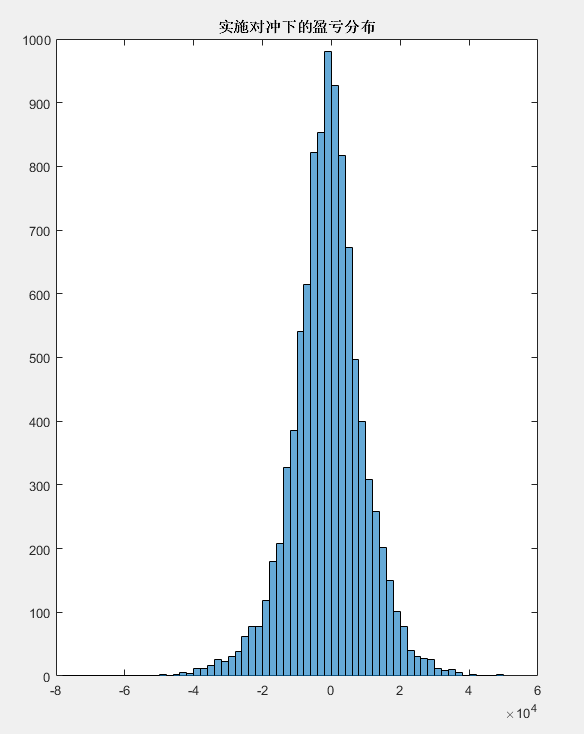
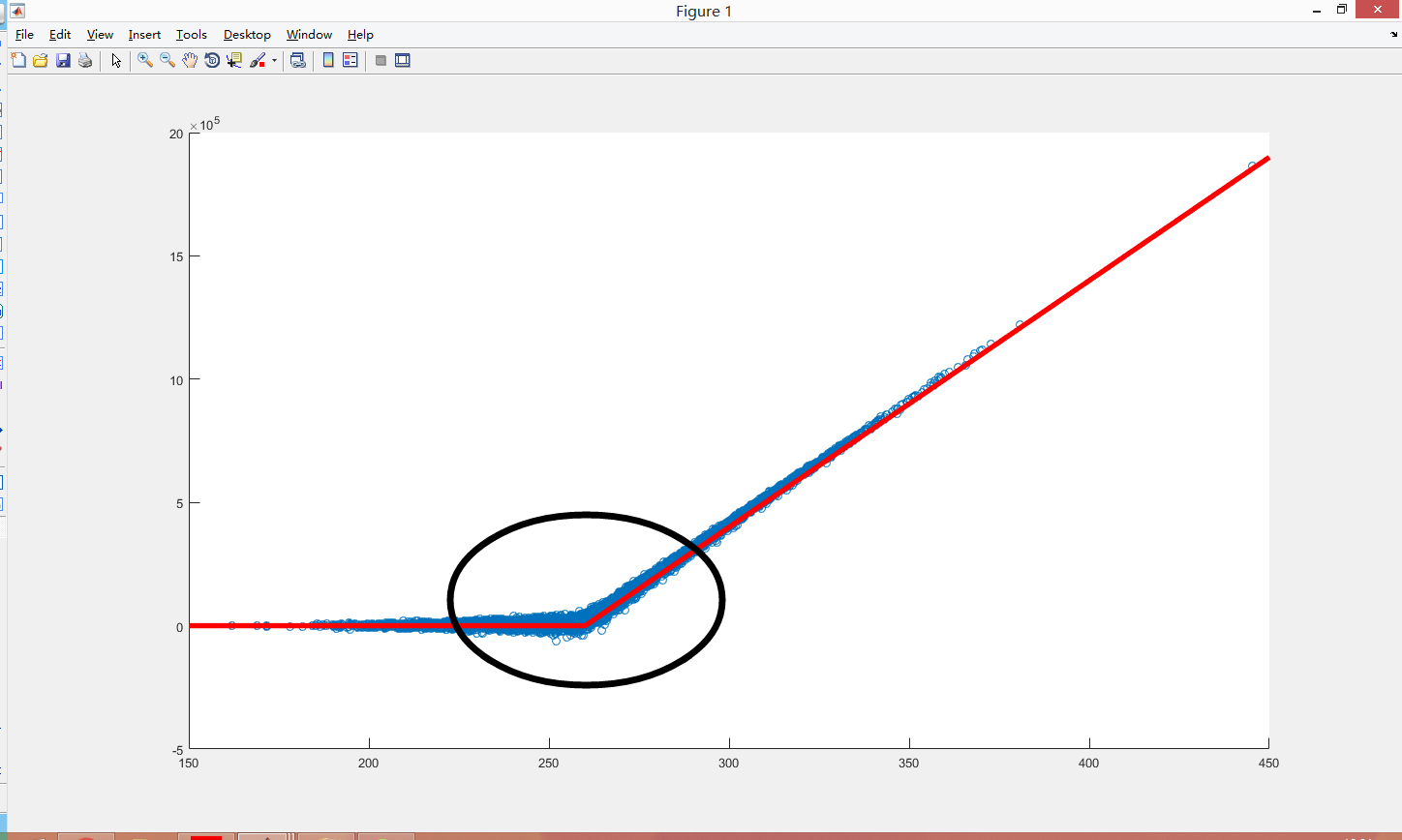
关于执行价附近离散情况比较严重的情况，请参见下图：
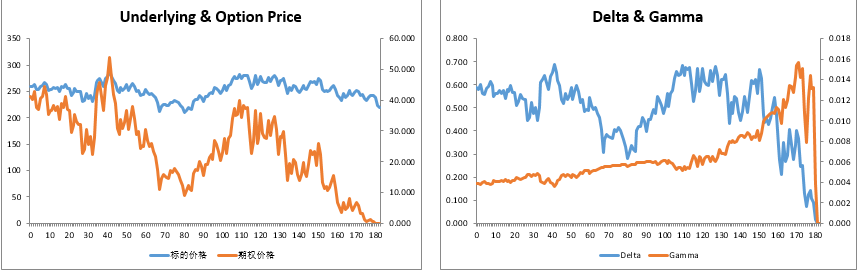由于标的价格在执行价附近波动的时候delta变动频繁，无法连续对冲导致对冲的时候容易被两边打脸造成亏损。尤其是临近到期日，假如标的价依然在执行价附近的话，Gamma变动会加剧，导致复制误差加大。
实际上，Delta对冲会面临如下问题：
1. 无法连续对冲导致的对冲误差。由于存在交易费用，因此对冲频率和交易费用二者在对冲交易的时候需要权衡。
2. 波动率样本误差。由于计算波动率的时候取样频率也是离散的，于是会产生样本误差。《Volatility Trading》一书，第二章中说到，一般波动率从的取样误差由下式给出：
3. 对冲路径依赖问题。由于对冲非连续的缘故，原本属于非方向性的对冲交易就变成了追涨杀跌，同样波动率的两条标的路径，对冲后的PnL会完全不一样。（这个通过上述回测就知道了。）
在量化研究（六）里面曾经提到过，Delta对冲后，资产组合的盈亏如下式：
留意到式子里面有个S的平方，因此Delta对冲后，总获利是依赖于股价的路径的。
关于对冲究竟用什么样的波动率，《Volatility Trading》里的第七章同样给出了建议：
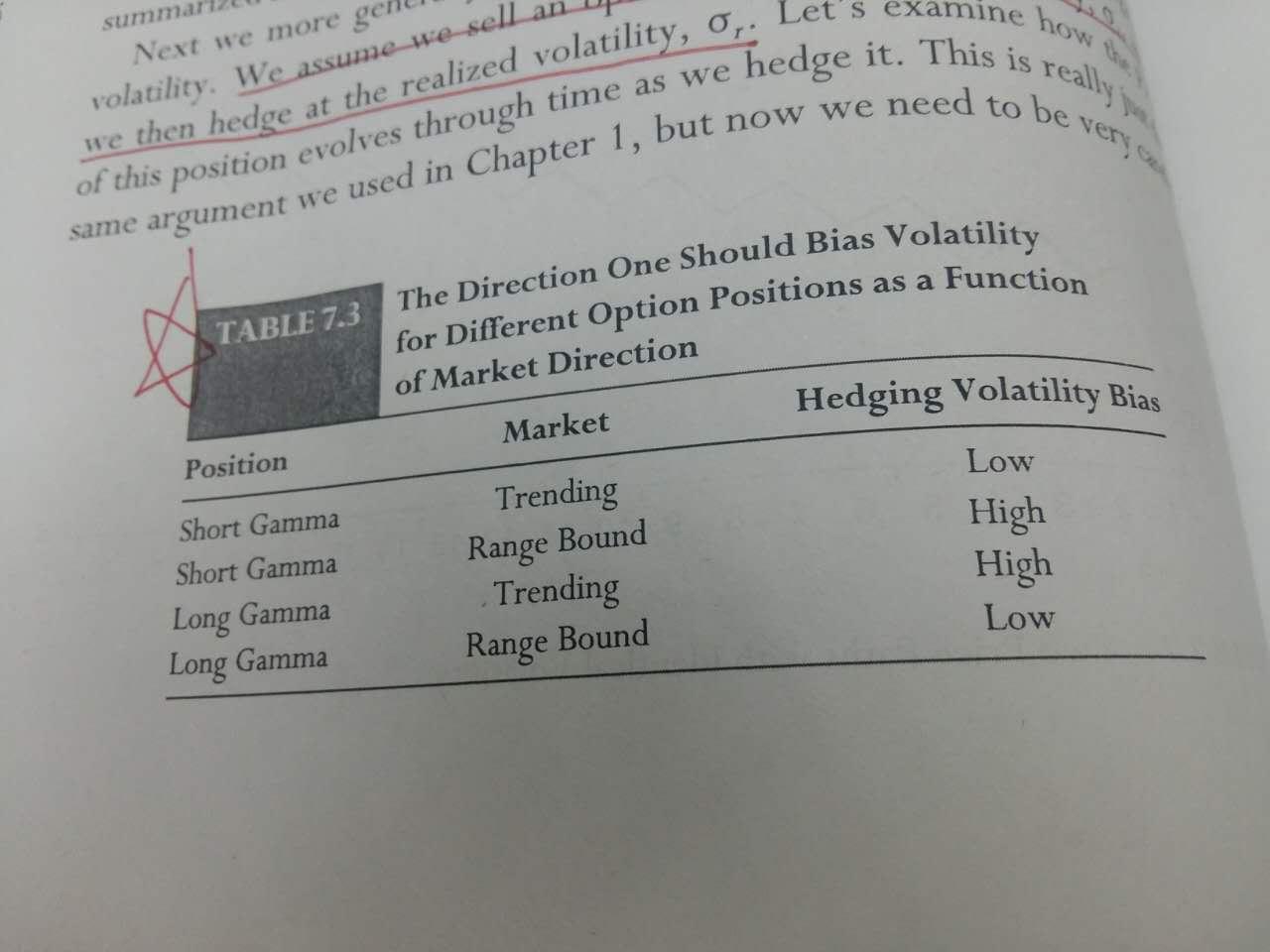对于期权卖方（Short Gamma）来说，遇上趋势行情，一般会调低波动率。遇上震荡行情，一般会调高波动率。
====== 以下是废话 ======
记得当时还在基金公司实习，正是找不到工作的时候。
当时在想着，这次实习可能是人生中最后一次做跟量化相关的工作了。
于是我特意买了一本笔记本，把每天的分析证明记下来。
好让我在去了银行做柜员之后，偶尔还能拿出来翻看，想着当年自己也牛逼过。
到了今天，专栏文章有一半内容都是当时做的笔记。
不知道这算不算天道酬勤的例子。
人生啊，确实要比当归大条一点。
======================
---
冼尼玛
2016/09/08
=========== 交易员崛起 · 专栏目录 ===========