原文

====== 正文之前来点不是废话的题外话 ======

一直都收到很多私信问关于金融工程学习的建议。

不管提问者是谁，我永远都会给出一个建议：看书最好看原版。

最近看的神书《Volatility Trading》，某部分看不太懂，于是翻看中文翻译版。

才发现中文翻译版居然把Implied Volatility Dynamic那一章很重要的部分全删了，真是无语。

另外翻译版的翻译质量也是十分参差，有些简直可以用垃圾来形容。

本屌在这里呼吁各位：

机械工业出版社出版的经济金融类翻译书籍（留意是经济金融类，其他类别的我不清楚）千万千万不要买。就是浪费钱。

中国人民大学出版社，以前的翻译质量还是很可以的。

但是自从看了他们翻译的伍德里奇的计量经济学导论之后，我有所保留。

说这么多，重点只有一个：看书最好看原版

====== 题外话说完 ======

====== 以下是正文 ======

上一篇量化研究，我们说了（历史）波动率分布与delta对冲之间的关系。

然而事情当然是没有那么简单的……

在多维度的的期权世界里，一张期权合约从价格A走到价格B，哪怕是忽略执行价这个固定因素，（至少）有5条路径可以走。还没算上变量自身的变化路径。

比如这篇文章要说到的Volatility Smile。

先简单解释一下波动率微笑Volatility Smile（一说Volatility Skew）。

在BSM的世界里，我们假设期权价格是标的价格与时间的函数，即V=V(S, t)。

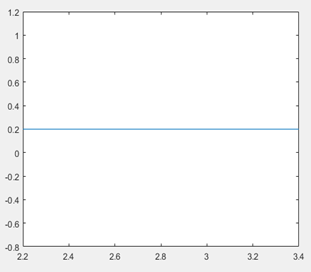
波动率在这里被假定为Constant的，也就是说假如以横坐标为在值状态（\frac{S}{K} ），纵坐标为波动率，在BSM世界里，画出来的图会是这个样子的：

就是一条平衡与X轴的直线。

但事实上并不是这样，下图是从Bloomberg上截取的50ETF波动率偏度图。

横坐标是Moneyness，纵坐标是ATM期权的Imp.Vol

橙色线是近月（9月），绿色线是次近月（10月）、蓝色线是季月（12月）。

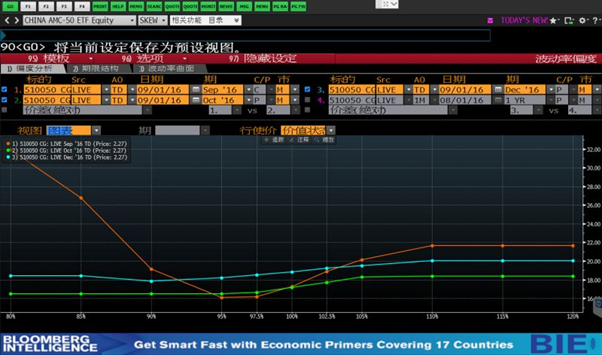
可以明显看到，近月的Skew十分明显，尤其是OTM期权的IV，高得离谱。

然而在次近月和季月，Skew几乎是平的，接近与BSM世界描述的情况。

没想到我大天朝在期权波动率方面已经超英赶美提早进入完备市场了可喜可贺啊……

咳……我们继续。



关于为什么会存在Skew，有如下几个解释（个人感觉第一种解释比较靠谱）：


关于Skew与标的价格之间的关系，有如下两个说法（就是我上文说的Volatility Trading翻译版删掉的部分）：Sticky Strike 与 Sticky Delta（或者叫Sticky Moneyness）。

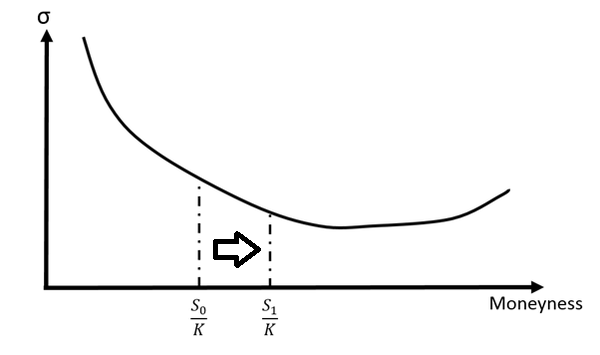
Sticky Strike的意思是，对于给定的执行价，期权的Vol与标的价格是独立的，也就是\frac{\partial \sigma(K) }{\partial S} =0。Sticky Strike用图形表示如下：

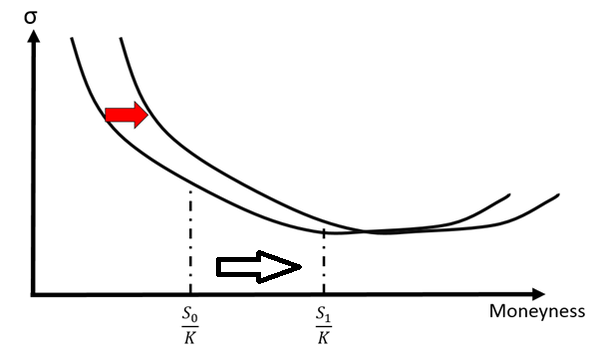
Sticky Delta（Moneyness）的意思是，对于给定的Delta（Moneyness），整个Skew的图形会随着标的价格的变动而变动，使得期权的Vol不变。即\frac{\partial \sigma(K) }{\partial \Delta } =0。Sticky Delta的变动如图所示：

Derman（1999）曾经在一篇高盛的研报里面研究了有关Stikcy Strike与Sticky Delta的特征：当行情处于震荡的时候，Skew的变化倾向于Sticky Srike。当行情处于趋势的时候，Skew的变化倾向与Sticky Delta

原文请戳：

Emanuel Derman

接下来说一下Sticky Strike下的套利。

在行情处于震荡期，即Sticky Strike期间，可以通过构造Call Spread + Delta Neutral的组合实现套利。数学证明如下：

假设无风险利率 r=0，市场上有两个Call，C_{1}(K_{1}), C_{2}(K_{2}) ，其中K_1>K_2

假设存在斜率为负的Vol.Skew，因此\sigma (K_1)<\sigma (K_2)

考虑如下的Call Spread：C_1(K_1)-\frac{\Gamma _{1} }{\Gamma _{2}} C_2(K_2)，其中\Gamma_1, \Gamma_2为两个Call各自的Gamma。

对上述的Call Spread进行Delta Neutral构造一个Delta中性的组合：

\Pi =C_1(K_1)-\frac{\Gamma_1}{\Gamma_2}C_2(K_2)-\Delta_p S

其中：\Delta_p=(\Delta_1-\frac{\Gamma_1}{\Gamma_2}\Delta_2)，是整个Call Spread的Delta。

对上述组合π做泰勒分解，瞬时PnL如下：

d\Pi =d(C_1(K_1))-\frac{\Gamma_1}{\Gamma_2}d(C_2(K_2))-\Delta_p dS =\Delta_1 dS+\frac{1}{2}\Gamma_1(dS)^{2}+\theta(K_1) dt-\frac{\Gamma_1}{\Gamma_2} (\Delta_2 dS+\frac{1}{2}\Gamma_2(dS)^{2}+\theta(K_2) dt)-(\Delta_1-\frac{\Gamma_1}{\Gamma_2}\Delta_2)dS
=\theta(K_1)dt-\frac{\Gamma_1}{\Gamma_2} \theta(K_2)dt

根据量化研究（五）里面Theta和Gamma的关系：\theta=\frac{1}{2}\Gamma S^{2} \sigma _{imp}^{2} 。

代入上式，整个组合的瞬时PnL就变成：

d\Pi =\frac{1}{2}\Gamma_1S^{2}(\sigma _{imp,K_2}^{2}-\sigma _{imp,K_1}^{2} ) dt

回到最上面关于Skew的假设，\sigma(K_1)<\sigma(K_2)，因此组合π的瞬时收益恒大于零。

当然上述基于数学的分析都是理论上的，实际上如果这么搞，要面临下面几个问题：

  1. Gamma的变动，震荡期间两个Call的Gamma一直在变动，因此有可能需要调仓，并且由于ATM的Gamma太大，不能搞那些太靠近ATM的期权。
  2. 上述分析的大前提是，你对行情震荡的判断是正确的。
  3. 上述分析还没考虑Vega。

之前咱们组的老大说卖Spread主要是赚Skew的钱。

今天总算有点明白了。

今天先写到这里，下次说一下Sticky Delta。




冼尼玛

2016/09/02

=========== 交易员崛起 · 专栏目录 ===========